Mathseeds White Paper

Executive Summary

Mathseeds is an innovative teaching and learning programme that focuses on the needs of pupils learning mathematics in kindergarten through grade 2. The programme has been carefully structured to support individual learning by combining pedagogical research on number sense, child development, technology, motivation, and key curriculum initiatives. Taking into consideration the needs, learning styles, and future direction of learners in the 21st century, Mathseeds combines a highly motivational play-based online context with structured, sequential mathematical lessons. At the core it is a teaching and learning sequence consisting of more than 140 lessons where key concepts in mathematics are taught, explored, practiced and assessed. Alongside the core lessons are fluency and assessment components, as well as rewards and a range of teacher resources to guide pupils toward their most successful mathematical future. It seamlessly connects learning between school and home across a range of computer devices. Teachers are able to monitor and report on both whole class and individual pupil progress, and provide useful feedback to pupils, parents, and other key stakeholders in their schools and districts. Mathseeds is carefully designed to motivate and maximize pupil learning to provide the strongest foundation to achieve lifelong mathematical success.

National Climate

The National Research Council’s significant reports Adding It Up (2001) and Mathematics Learning in Early Childhood (2009) represent mathematics as a complex domain. They advocate a multifaceted approach to meet the needs of a broad range of pupils in classrooms across the United States. The collaborative position paper by the National Council of Teachers of Mathematics and the National Association for the Education of Young Children, Early Childhood Mathematics: Promoting Good Beginnings `(2010) stresses to stakeholders the role that comprehensive early childhood mathematics has in developing lifelong learners of mathematics. It outlines recommendations at classroom, community, and systemic levels to promote collaboration for optimal learning outcomes.

The Council of Chief State School Officers reviewed these key documents and took on the challenge to improve school mathematics by developing the Common Core State Standards for Mathematics (CCSSM). Success in implementing a mathematics programme based on the pedagogical research and the CCSSM requires three essential shifts. Teachers need to focus on fewer content areas, on connecting ideas; and maintaining high levels of expectations for learning. Mathseeds provides teachers and parents with research-based materials that support these key shifts for kindergarten to grade 2 pupils. Each Mathseeds lesson provides exploration, practice, and application in one or more aspects of number sense, operations and algebraic thinking, measurement, data, and geometry.

Number Sense

“

Number sense … shapes children’s mathematical futures and potentially their life chances, from their earliest engagement with mathematical learning. ”

Children develop their mathematical abilities following natural learning progressions with number sense being a formative platform for numeracy success (Clements & Sarama, 2009; Klibanoff, Levine, Huttenlocher, Vasilyeva & Hedges, 2006; NCTM & NAEYC, 2010). Broadly, number sense is the "understanding of number needed by children if they are to succeed in mathematics" (Howell & Kemp, 2006). It encapsulates counting abilities, number patterns, estimation; sequencing, connecting counting to cardinality, and number manipulation.

In their research, Cain, Doggett, Faulkner & Hale (2007) outline seven key elements that are core to number sense. Figure 1 shows these components: quantity/magnitude, numeration, equality, base ten, form of a number, proportional reasoning, and algebraic and geometric thinking. Faulkner (2009) asserts that ultimately these components of number sense operate as a useful framework in visualizing the interconnectedness of the principles of mathematics. It is important to view this not as a progressive model but rather to see that each component is connected and integral to each lesson.

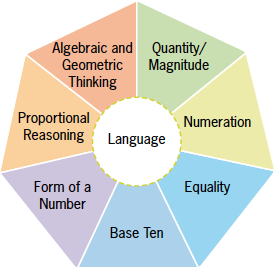
Figure 1: Cain and colleagues (2007) identified seven core components of number sense.

Strong number sense has been shown as a precursor of future mathematical success (Jordan, Kaplan, Locuniak & Ramineni, 2007) with the suggestion it may prove to be to mathematics what phonemic awareness is to reading (Gersten & Chard, 1999). To help nurture the natural learning progress of number sense, pupils need to explore numbers and engage with them using multiple presentations and a wide variety of different activity types.

Mathseeds recognizes the importance of number sense and the strong developmental role it has for setting the most successful trajectory in mathematics. It situates number sense activities in scenarios that are familiar, such as playgrounds, kitchens for cooking, and shopping adventures. In doing this Mathseeds provides a playful environment to explore and interpret the quantitative concepts of number sense. This playful format also allows for number sense concepts to be presented and explored by pupils in a variety of ways. The sequence of lessons in Mathseeds supports children by continually revisiting concepts and building on earlier skills in a way that deepens their understanding. This provides a strong foundation for more complex mathematical processes to come.

Programme Features

Key Elements

Research has indicated that several principles and critical factors underpin the most effective mathematical pedagogy and instruction. These principles include motivation and engagement, building on pupil’s thinking, making connections, structured lessons, tools and representations, feedback, and assessment for learning (Anthony, & Walshaw, 2009; Jensen, 2005; NCTM & NAEYC, 2000; Sullivan, 2011). Mathseeds combines each of these into an engaging environment for young children. The programme focuses on pupil interaction and features a wide variety of short instructional movies and highly motivating activities. Students continually earn rewards which encourages active participation.

All Mathseeds lessons follow a similar structure. Each lesson focuses on a particular mathematical competency, with instructional lessons being taught by one of the five key characters. The programme offers pupils opportunities to engage in practice and review activities, with up to 12 parts. Initial lessons build on the pupils’ early mathematical experiences and focus on developing number sense (NCTM, 2000; Perry, 2000). Other lessons focus on operations and algebra, geometry, measurement, and data (NCTM 2000).

Mathseeds Lesson 14 has 12 instructional parts and activities. The lesson introduces the number eight. It has as a strong instructional focus on the early skill of one-to-one correspondence which is an important prerequisite to rational counting (Reys, Lindquist, Lambdin & Smith, 2012). Figure 2 shows this teaching activity in action. Mango the monkey and Silky the spider help children identify the number eight visually and by name. Various activities follow that reinforce the number’s name and shape, and pupils identify number eight both in isolation and when presented as one of three other numbers. Students count one item at a time to reinforce the concept of cardinality. Figure 3 shows this teaching activity in action.

Figure 2: Lesson 14, narrator is guiding pupil through one-to-one correspondence.

Figure 3: Lesson 14, narrator is guiding pupil through one-to-one correspondence.

After the initial lesson animations, Lesson 14 continues with a variety of interactive activities that focus on number identification, number formation, number name recognition, number lines, sorting, and counting. The final learning activity is the e-book which recaps what has been learned and acts like a plenary for each Mathseeds lesson to consolidate new concepts and skills. The final part of each lesson is a pet-hatching animation. Each lesson ends with the hatching of a unique pet that is added to the Mathseeds map. This is a highly motivational element for children who look forward to seeing which animal will be next. These hatching pets act as both a reward for lesson completion and also encourage children to proceed to the next lesson in the programme. In addition to the core lessons, the Driving Test area of the programme offers a wide range of tests that assess skills and knowledge in number, operations, patterns, measurement, geometry, and data. While the Number Facts area of the programme focuses on building fluency with basic facts, this section brings mental arithmetic to life, where pupils can engage in a huge range of fun activities that develop number fact fluency.

Active Engagement

“

Mathematics is not only taught because it is useful. It should be a source of delight and wonder, offering pupils intellectual excitement and an appreciation of its essential creativity. ”

Research indicates that mathematical engagement occurs when pupils enjoy the subject of mathematics, value their mathematics learning, and see the relevance of it in their lives. The ability to make connections between the mathematics that is taught in class and the mathematics that is applied in the outside world is crucial (Attard, 2012; Roschelle, Pea, Hoadley, Gordin & Means, 2000). Similarly, Willis (2014) has stated that "Relevance increases engagement and reduces boredom when pupils recognize instruction as related to their interests…" (p.30). It is engagement, rather than memorization tasks that activates more pleasure structures in the brain (Poldrack, Clark, Pare-Blagoev, Shohamy, Creso Moyano, Myers & Gluck, 2001).

In recognizing the importance of this research, the lessons and Playroom activities encourage pupils to make connections between their experience of the real world and mathematical thinking. Anthony & Walshaw (2009) in their research commented how:

"Making connections across mathematical topics is important for developing conceptual understanding… When pupils find they can use mathematics as a tool for solving significant problems in their everyday lives, they begin to view the subject as relevant and interesting." (p.156)

New skills and concepts are taught in a context that is relevant, familiar, and of interest to most young children. From choosing the correct bus as it drives by, to feeding birds the correct number of worms in a bird café, to getting an astronaut back to his rocket ship, the Mathseeds activities bring mathematical concepts to life. And with more than 350 different activities, pupils are always seeing content that is new and interesting. For pupils working through the programme, the Mathseeds lessons and activities are all set in a nonthreatening environment that supports risk taking and rewards perseverance.

Instructional Formats

“

Over the past decade a suite of studies focused on the early bases of mathematical abstraction and generalisation has indicated that an awareness of mathematical pattern and structure is both critical and salient to mathematical development among young children.. ”

At the core of Mathseeds are the instructional movies and interactive activities that make up the beginning of each lesson. Both the movies and activities have been purposely designed to encourage active learning rather than what Roschelle and his colleagues referred to as the "passive role of receiving information" (2000, p.79). Evidence supports the belief that pupils learn best when they are provided with short sessions, a quick instructional pace, and time to process new information (Fuchs & Fuchs, 2001; Jensen, 2005). As shown in Figure 4, Jensen (2005) recommends 5-8 minutes direct instruction for early elementary school pupils. The Mathseeds instructional video sequence is interspersed with short, interactive activities that serve as practice and consolidation, as well as a method for keeping pupils focused.

Figure 4: Jensen (2005) identified appropriate durations for direct instruction for children.

The Mathseeds Playroom contains several activities that have been designed for young children. They are a combination of open-ended tasks, such as stamping shapes to create a picture, or specific tasks such as popping balloons on a 0–9 number line. Figures 5–8 show these learning activities in action. The activities take into consideration the short concentration spans of young children, but several activities loop for as long as the child wants to engage and play.

Figure 5: Playroom, pupils continue simple patterns.

Figure 6: Playroom, pupils are playing with cardinality.

Figure 7: Playroom, pupils are exploring measurement.

Figure 8: Playroom, pupils are identifying numbers and coloring.

“

Representations are key tools for mathematical learning, particularly the use of linked multiple representations. Often conceptual understanding comes through recognising representations and the connections between them. ”

Interactive activities are by their nature, more compelling than paper and pencil activities. A study by Moyer, Niezgoda & Stanley (2005) revealed the high level of creativity and complexity demonstrated by kindergarten pupils using virtual manipulatives and software as opposed to concrete materials. Mathseeds lessons use short and varied activities to maintain pupil interest and regular rewards to g motivation. The activities are playful so that pupils see them as an extension of how they play—and this means pupils are more likely to be fully involved and immersed in the activity, which also helps to build stronger connections and boost memory retention of new skills. Many of the Mathseeds instructional movies end with a song. This acts as an additional way for pupils to remember mathematical concepts in a fun and engaging way (Hayes, 2009; Jensen 2005).

One important feature of the Mathseeds instructional format is that on completion of every activity, the pupil receives immediate encouragement, feedback, and error correction in a nonthreatening way. Feedback in the early stages of learning is essential for keeping pupils on track and focused (Garnett, 2005; Griffith & Burns, 2012; Jensen, 2005). Hattie and Timperley (2007) reveal that "… the most effective forms of feedback provide cues or reinforcement to learners… in the form of video-, audio-, or computer-assisted instructional feedback…" (p.84). This view is shared by Roschelle et al. (2000), who confirm that computer technology encourages rapid interaction and feedback. Students who receive this type of prompt feedback are more likely to be motivated to continue (Fuchs & Fuchs, 2001).

The interactive activities that follow each lesson give pupils vital opportunities to review, revise, and repeat new skills (Jensen, 2005). They allow pupils to build on their knowledge and see the links between mathematical ideas, as evidenced as important by Anthony & Walshaw (2009). In keeping with the concept of a spiral curriculum (Bruner, 1960), the Mathseeds programme is structured so that ideas introduced in early lessons are later revisited at a more advanced level. Mathematical vocabulary is introduced early in order to prepare pupils for future, more complex learning (Anthony & Walshaw, 2009; Jensen, 2005).

Learning Styles and Multiple Intelligences

“

Pluralisation achieves two important goals: when a topic is taught in multiple ways, one reaches more students. Additionally, the multiple modes of delivery convey what it means to understand something well. When one has a thorough understanding of a topic, one can typically think of it in several ways, thereby making use of one’s multiple intelligences. ”

Much has been written regarding individual learning styles and multiple intelligences; their importance and implications for learning (Adams, 2000; Bloom 1956, Clausen-May, 2005; Green, 1999; Tiberius & Tipping, 1990). The work of Gardner (2011) identifies the variety of intelligences that pupils apply in learning situations, highlighting the fact that not all children learn in the same way and require programmes that reflect their different approaches to learning (Adams, 2000). The scope of Gardner’s work on discrete multiple intelligences is demonstrated by Figure 9. Educators can engage with the widest possible audience when they design activities that utilize their pupils' broad range of intelligences.

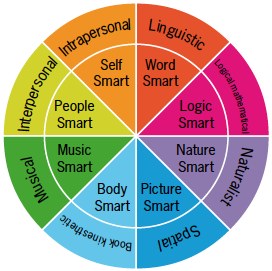
Figure 9: Howard Gardner’s Multiple Intelligences

Mathseeds is designed to appeal to different learning styles and multiple intelligences. The programme’s content and variety allow all pupils the opportunity to engage in mathematical learning. The following examples illustrate how Mathseeds caters for multiple intelligences.

Logical/Mathematical

Mathseeds appeals to those who think logically. There are opportunities within the programme for pupils to calculate answers, solve problems with numbers, draw conclusions, explore the relationships between numbers, shapes, and statistical data, work with different representations of numbers, and gather and interpret information.

Verbal/Linguistic

The programme offers opportunities for seeing, saying, counting, reading, and writing numbers. The Mathseeds Playroom also offers opportunities for young children to hear and sing along with familiar nursery rhymes that reinforce counting and simple mathematical concepts such as days of the week.

Throughout the programme, children are encouraged to listen and follow instructions. There are opportunities to read and comprehend word problems and explore ways of converting problems to algebraic expressions. Mathseeds characters expose pupils to new mathematical expressions and help them to explore mathematical vocabulary. Research indicates that these aspects should be modeled in order to enhance pupils’ understanding (Runesson, 2005). At the end of each lesson, pupils can read e-books that consolidate new concepts. The texts are professionally narrated which provides a model for the child’s own reading fluency. Figure 10 shows the layout and content for the e-book Near Doubles for Lesson 91.

Figure 10: Lesson 91, Near doubles e-book

Visual/Spatial

The Mathseeds programme features high-quality, colorful animations that have been designed to appeal to the visual learner. The onscreen graphics are bold, clear, and engaging. Lesson progression is mapped in a fun and unique way. Students are taken to a range of virtual habitats. Stepping stones mark their progress through each habitat, and on completion of each lesson, pupils move forward to the next stepping stone. This creates a very powerful and visual way of helping pupils see the progress they are making and ensures that they stay motivated toward their goals. Making progress visible to pupils is articulated in research as being a key goal (Adams & Hamm, 2014; Marzano, 2007; McLennan & Peel, 2008).

In addition, each Mathseeds lesson is accompanied by an e-book with full-colour illustrations. The programme also has accompanying posters and worksheets to consolidate learning and increase information processing.

Bodily/Kinesthetic

Mathseeds offers kinesthetic learners the ability to engage their senses and create an experience that goes beyond simply learning by rote which Clausen-May (2005) identifies as crucial. Early number concepts are taught in a very visual and kinesthetic way and encourage pupils to see numbers as wholes. The first Mathseeds song, "There Is Only One of Me," encourages the pupil to see and feel that they have only one nose, one face, one mouth, etc.

Bobis (2008) in her research identifies how virtual manipulatives can assist pupils with number sense and spatial thinking. In Mathseeds pupils are encouraged to subitize early on and the presence of dominoes, dots, and various other engaging items to count are available for all pupils to use— not just the kinesthetic learners. Research indicates that when given the appropriate materials, pupils can mentally combine and partition numbers. This is an important skill prior to the introduction of addition and subtraction (Bobis, 2008).

Early addition lessons physically show the main character joining two distinct subgroup together to form one group, or total. Only when this concept of addition is in place does the programme present addition in the form of a simple number sentence and eventually as a formal algorithm. Figures 11–13 demonstrate the sequential building of this conceptual knowledge.

Figure 11: Lesson 24, characters are exploring two distinct groups and joining them together to find the total.

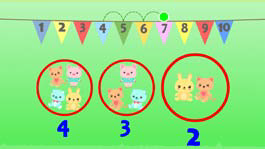
Figure 12: Lesson 51, characters are adding and locating the final counted numeral as the total on a number line.

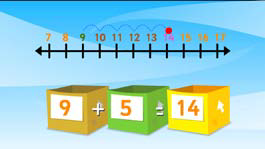
Figure 13: Lesson 65, characters are creating formal number sentences from pictorial representations.

Similarly, subtraction is taught through more than one approach. Students physically take items away from the main group when learning how to subtract. They also learn to cover items up, and eventually progress to counting back along a number line, using subtraction number sentences and finally formal algorithms. This multilevel and kinesthetic approach allows pupils to understand why a method works, rather than how to just solve a problem (Clausen-May, 2005).

Musical

“

Play and learning maths do not have to be mutually exclusive events. Play and games can give young children opportunities to learn and develop foundational math skills. ”

Mathseeds is full of playful songs that act as mnemonics to aid memory and consolidate new concepts. The songs are popular among children and perfect for those who have sensitivity to music. The Mathseeds Playroom has a number of traditional nursery rhymes and familiar songs that reinforce simple counting skills and other mathematical ideas.

Aspects of rhythm are also used to teach mathematical concepts such as patterning. According to Mulligan (2010), "an awareness of mathematical pattern and structure is both critical and salient to mathematical development" (p.47). In Mathseeds pupils are encouraged to participate in simple dances, led by the onscreen characters, to demonstrate the idea of repeating patterns. Figure 14 is an example of one such song from Lesson 66 about fractions.

Figure 14: Lesson 66, characters singing a fraction song about quarters.

Interpersonal/Intrapersonal

The Mathseeds programme can be used in a variety of ways to promote interpersonal and intrapersonal skills. It can be used with a whole class or for a focused group lesson. It encourages talk and discussion, sharing, and group participation. The programme can also be used on an individual basis for pupils who prefer to work alone at their own pace. It allows for thoughtful reflection on individual progress.

Mathseeds lessons encourage pupils to think about how they use mathematics outside of the lesson. This provides opportunities for pupils to draw on their own experiences and construct their understandings of the real world (NCTM, 2000; Perry, 2000; Tiberius & Tipping, 1990). In Mathseeds the onscreen characters model how to solve problems through discussion and rationalizing. They effectively teach pupils how to monitor the problem-solving process and demonstrate for pupils how a collaborative atmosphere enhances learning.

Motivational Elements

“

In order to become capable and strategic learners in mathematics, pupils need to have confidence in their own ability and self-identity as learners of mathematics. Strategies that promote inclusiveness, deep thinking, and ownership, can have a powerful effect on building pupils’ mathematics skills. ”

“

Raising pupil attainment in mathematics is one of those things that is so easy to say, yet is so difficult to achieve, and sustain. In short, it is an enduring challenge in most mathematics classrooms. ”

When addressing the issue of how to interest and engage pupils, Sullivan and McDonough (2007) refer to the pupil’s "willingness to persist" (p.698). This "willingness" is the motivation required for pupils to complete learning activities. Motivation plays a key role in learning (Gagne & Deci, 2005; Jensen, 2005; Rodionov & Dedovets, 2011; Sullivan & McDonough, 2007; Taylor & Adelman, 1999). Intrinsic motivation rewards pupils purely for participating in the activity itself, whereas extrinsic motivation is derived from gaining awards such as certificates or verbal rewards (Gagne & Deci, 2005; Ryan & Deci, 2000). These important, positive rewards impact pupil motivation (Griffith & Burns, 2012; Jensen, 2005). Mathseeds seeks to provide both intrinsic and extrinsic motivational rewards in order to produce total satisfaction.

Rewards reinforce existing learning and encourage new learning to occur. The brain responds favorably to rewards, the potential for rewards (prediction) and to unexpected rewards (surprise). It releases a sudden burst of dopamine that makes the pupil feel good and motivated to continue with the task (Bear, Connors & Paradiso, 2007; Jensen, 2005).

The Mathseeds programme rewards pupils with a cute pet that hatches from an acorn at the end of each lesson sequence. The first time this happens is an unexpected surprise for the pupil. After subsequent lessons the pupil knows it will happen (prediction) but they still have the element of surprise as they do not know what each pet will be until it hatches.

According to Edward de Bono, "Humor is by far the most significant activity of the human brain" (de Bono cited by Griffith & Burns, 2012). The Mathseeds programme actively motivates pupils through its elements of humor and playfulness. Each hatching pet has its own unique character that pupils can enjoy. In addition, the five key characters are role models for pupils; exploring new mathematical challenges and having fun whilst they learn.

Learning is an ongoing, dynamic process and the learning environment must continuously change to reflect this (Taylor & Adelman, 1999). The Mathseeds programme moves through different locations, with regard to the lessons and reward maps. The key characters remain the same but they present the lessons intermittently to maintain pupil interest. The huge range of interactive activities are uniquely written and animated in different styles to prevent pupils from becoming bored and demotivated.

According to Taylor & Adelman (1999), "One of the most powerful factors for keeping a person on task is the expectation of feeling some sense of satisfaction when the task is completed" (p.266). Mathseeds rewards pupils with golden acorns at the completion of each lesson and activity. These get banked and can later be spent on clothes for the pupil’s avatar (online character) or furniture for their personal tree house.

After the completion of five lessons, pupils participate in an online quiz. If they pass, their efforts are rewarded with a printable gold, silver, or bronze certificate with their name on it. Providing a representation of a very personal accomplishment can be a valuable motivator to improve pupil achievement (Marzano, Pickering & Pollock, 2001). The range of rewards that Mathseeds offers pupils actively encourages them to engage with the programme, explore it, learn from it, and value their progress.

Assessment

“

I am more and more convinced of a need for planned consolidation, so that after every mathematical task, whether it was a practice exercise, a problem-solving activity, a game, or whatever, there needs to be some kind of interaction that reviews the core mathematical idea, together with its language, and its representations, and focuses on how it arose and how it might be recognised in future. ”

Assessment is necessary to monitor progress, to identify strengths and weaknesses, and to inform further instruction. Mathseeds provides multiple opportunities for informal assessment. Games offer immediate, interactive reporting directly to pupils; they know instantly if they are correct. Following this feedback, teachers can focus on an area where a pupil had difficulty by asking him or her to describe the concept or process.

Mathseeds also has a more formal assessment system built into the programme. After each online activity, the results are uploaded to the parents’ and teachers’ dashboards, mobilizing continual progress reporting. In an assessment system that weaves through the entire multilevel programme, parents, teachers, and pupils are offered strong, constructive feedback in positive forms that encourage further development and growth.

It is essential to have a range of both summative and formative assessment opportunities to enable teachers to make balanced judgements on the understanding of pupils across key mathematical skills. These assessments should present pupils with multiple avenues to show their knowledge and have distinct structures to cater for a wide range of pupils. At the end of a map of five lessons, pupils complete a 15 question assessment quiz that assesses their understanding of the content covered in the previous five lessons. Students receive merit certificates based on their score.

Mathseeds assesses pupil progress with regular Driving tests, which are 10 question tests that assess pupil knowledge in essential mathematics skills. These assessments have responsive feedback that requires pupils to redo questions they get incorrect. This allows pupils to critically evaluate incorrect responses to reinforce correct mathematical thinking. Teachers receive detailed feedback on all attempts and this gives them valuable information about their pupils' mathematical reasoning.

Another assessment component can be found in the teacher console, where teachers can choose from a range of standards-based assessment tasks that can be assigned to individual pupils, groups or the whole class.

This suite of assessment tasks provides teachers with the necessary tools they need to track pupil progress and to inform their teaching. Its rich, useable assessment data means Mathseeds can easily be integrated into a range of teaching and learning programmes. As an interactive reporting programme it allows teachers to focus on particular data sets. This data might illuminate class weaknesses to inform small-group instruction or reveal strengths where pupils need to be extended beyond the grade’s standards. The aim is to make assessment data accessible to ensure it informs the teaching and learning process.

Technology

“

One of the chief benefits of mobile devices is that they enable learning anywhere, anytime. This allows a shift away from the industrial era model where the classroom is the central place of learning driven by the teacher and limited to instruction within the school day. In deploying mobile devices, the teacher is no longer at the centre of the learning process and the instructional time can transcend the school day. ”

As technology permeates all aspects of interactions, it has become "an ubiquitous tool for teaching and learning" (Li & Ma, 2010, p.215). The National Council of Teachers of Mathematics explicitly state technology as central in teaching and learning mathematics as it "influences the mathematics that is taught and enhances pupils’ learning’’ (NCTM & NAEYC, 2010).

Cheung & Slavin (2013) identify that as technology permeates 21st century living, the question for teachers shouldn’t be whether to use educational technology but rather what applications ensure it is in the best way for pupils (p.102). Technology that enables the manipulation of virtual objects is powerful (Hoyles & Noss, 2009), as are regenerative question designs that afford endless practice opportunities. By its design, the Mathseeds programme takes advantage of the inherent benefits of computer technology.

The programme allows children to manipulate objects in a variety of ways, to experiment without fear of failure and test out their new skills through a range of practice opportunities. Accessible on desktop and mobile devices, it bridges the home and school divide working to connect family and school communities in the learning process.

Research indicates the most powerful potential for tools are where meaningful interactions operate alongside sound teaching and learning strategies (Coley, Cradler & Engel, 2000) and guided support (Moyer et al., 2005). Mathseeds is an innovative interactive teaching and learning resource designed by educators to connect pupils to the key concepts of number sense. In teaching and learning sequences, pupils play with virtual manipulatives in short, focused sequences. This teaching is always linked to content in the lesson that follows and is a scaffold to provide guided support for activities within the lesson sequence.

Conclusion

Mathseeds is an interactive Web-based programme that incorporates a huge range of highly structured, effective, research-based activities. It combines rigorous learning with high-interest level activities, taking into consideration the needs, learning styles, and future direction of learners in the 21st century. Mathseeds has been built on best practices in pedagogical research alongside core curriculum initiatives, creating a programme that is both educationally sound and highly motivating. Mathseeds lessons provide an engaging environment for young children who learn best through play. The instructional elements and interactive activities are set in contexts that are meaningful and relevant. The programme offers a range of age-appropriate rewards that actively encourage pupils to engage with the programme, explore it, learn from it, and value their progress.

Mathseeds is designed to seamlessly connect learning between school and home, making learning possible anywhere and easily accessible on different devices. Its comprehensive assessment and reporting procedures allow pupils, parents, and teachers to receive instant feedback on progress and achievements made. Written by experts with over 25 years of experience in creating high-quality educational resources, Mathseeds has been carefully designed to maximize pupil learning and to equip pupils with the strongest foundation possible to achieve lifelong mathematical success.

References

Adams, T. L. (2000). Helping children learn mathematics through multiple intelligences and standards for school mathematics. Childhood Education, 77, (2), 86–94.

Adams, D. & Hamm, M. (2014). Teaching math, science and technology in schools today: Guidelines for engaging both eager and reluctant learners. Plymouth: Rowman & Littlefield Education.

Anthony, G., & Walshaw, M. (2009). Characteristics of effective teaching of mathematics: A view from the West. Journal of Mathematics Education, 2 (2), 147–164.

Attard, C. (2012). Engagement with mathematics: What does it mean and what does it look like? Australian Primary Mathematics Classroom, 17 (1), 9–13.

Bear, M., Connors, B. & Paradiso, M. (2001). Neuroscience. Exploring the brain. Baltimore, MD: Lippincott Williams & Wilkins.

Bloom, B. (1956). Taxonomy of educational objectives. New York: David Mackay.

Bobis, J. (2008). Early spatial thinking and the development of number sense. Australian Primary Mathematics Classroom, 13 (3), 4–9.

Bruner, J. (1960). The Process of Education. Cambridge: Harvard University Press.

Cain, C., Doggett, M., Faulkner, V., & Hale, C. (2007). The components of number sense. Raleigh, NC: NC Math Foundations Training, Exceptional Children’s Division of the North Carolina Department of Public Instruction (NCDPI).

Cheung, A. C. K. & Slavin, R. E. (2013). The effectiveness of educational technology applications for enhancing mathematics achievement in K–12 classrooms: A meta-analysis. Educational Research Review, 9, 88–113.

Clausen-May, T. (2005). Teaching maths to pupils with different learning styles. London: Paul Chapman Publishing.

Clements, D. & Sarama, J. (2009). Learning and teaching early math: The learning trajectories approach. New York: Routledge.

Coley, R., Cradleer, J. & Engel, P.K. (2000). Computers and the classroom: The status of technology in U.S schools. Princeton: Policy Information Center, Educational Testing Service.

Cross, C. T., Woods, T. A. & Schweingruber, H. (Eds.) Mathematics learning in early childhood: Paths toward excellence and equity. Washington, D.C.: National Academy Press.

Edelson, D. C., & Joseph, D. M. (2001). Motivating educational psychology interactive. Valdosta, GA: Valdosta State University.

Faulkner, V. N. (2009). The components of number sense: An instructional model for teachers. Teaching Exceptional Children, 41 (5), 24–30.

Fredricks, J., McColskey, W., Meli, J., Mordica, J., Montrosse, B., and Mooney, K. (2011). Measuring student engagement in upper elementary through high school: A description of 21 instruments. (Issues & Answers Report, REL 2011–No. 098). Washington, D.C: U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southeast.

Fuchs, L. S., & Fuchs, D. (2001). Principles for the prevention and intervention of mathematics difficulties. Learning Disabilities Research & Practice, 16 (2), 85–95. Gagné, M. & Deci, E. L. (2005). Self-determination theory and work motivation. Journal of Organized Behavior, 26, 331–362.

Gardner, H. (2011). Frames of mind: The theory of multiple intelligences (3rd ed.). New York: Basic Books.

Garnett, S. (2005). Using brainpower in the classroom: Five steps to accelerate learning. London: Routledge.

Gersten, R. & Chard, D. J. (1999). Number sense: Rethinking math instruction for students with learning disabilities. The Journal of Special Education, 33, 18–28. Green, F. E. (1999). Brain and learning research: Implications for meeting the needs of diverse learners. Education, 111 (4), 682–687.

Griffith, A. & Burns, M. (2012). Outstanding teaching: Engaging learners. Wales: Crown House Publishing.

Hayes, O. C. (2009). The use of melodic and rhythmic mnemonics to improve memory and recall in elementary students in the content areas. Unpublished Ph.D., Dominican University of California.

Hattie, J. & Timperley, H. (2007). The power of feedback. Review of Educational Research, 77 (1), 81–112.

Highfield, K. & Mulligan, J. (2007). The role of dynamic interactive technological tools in preschoolers’ mathematical patterning. In J. Watson & K. Beswick (Eds.), Mathematics: Essential research, essential practice (pp.372–381). Adelaide: Mathematics Education Research Group of Australasia Inc.

House, J. D. (2006). Mathematics beliefs and achievement of elementary school students in Japan and the United States: Results from the third international mathematics and science study. The Journal of Genetic Psychology, 167 (1), 31–45.

Howell, S. & Kemp, C. (2009). An international perspective of early number sense: Identifying components predictive of difficulties in early mathematics achievement. Australian Journal of Learning Disabilities, 11 (4), 197–207.

Hoyles, C. & Noss, R. (2009). The technological mediation of mathematics and its learning. Human Development, 52, 129–147.

Jensen, E. (2005). Teaching with the brain in mind. Alexandria, VA: Association for Supervision & Curriculum Development.

Jordan, N. C., Glutting, J. & Ramineni, C. (2009). The importance of number sense to mathematics achievement in first and third grades. Learning and Individual Differences, 20, 82–88.

Jordan, N. C., Kaplan, N., Locuniak, M. N. & Ramineni, C. (2007). Predicting first-grade math achievement from developmental number sense trajectories. Learning Disabilities Research & Practice, 22 (1), 36–46.

Kilpatrick, J., Swafford, J. & Findell, B. (Eds.) Adding it up: Helping children learn mathematics. Washington, D.C.: National Academy Press.

Klibanoff, R. S., Levine, S. C., Huttenlocher, J., Vasilyeva, M. & Hedges, L. V. (2006). Preschool children’s mathematical knowledge: The effect of teacher “Math Talk”. Developmental Psychology, 42 (1), 59–69.

Li, Q. & Ma, X. (2010). A meta-analysis of the effect of computer technology on school students’ mathematics learning. Educational Psychology Review, 22 (3), 215–243.

Manner, B. (2001). Learning styles and multiple intelligences in students. Journal of College Science Teaching, 30 (6), 390–393.

Marzano, R. J. (2007). The art and science of teaching: A comprehensive framework for effective instruction. Alexandria, VA: Association for Supervision and Curriculum Development.

Marzano, R. J., Pickering, D. J., & Pollock, J. E. (2001). Classroom instruction that works: Research-based strategies for increasing student achievement. Alexandria, VA: Association for Supervision and Curriculum Development.

McLennan, B. & Peel, K. (2008). Motivational pedagogy: Locking in the learning. The Australian Education Leader, 30 (1), 22–27.

Moyer, P., Niezgoda, D. & Stanley, M. (2005). Young children’s use of virtual manipulatives and other forms of mathematical representation. In W. Masalski & P. Elliott (Eds.), Technology-supported mathematics learning environments (pp. 17–34). Reston: NCTM.

Mulligan, J. T. (2010). Reconceptualising early mathematics learning. In C. Glascodine and K. Hoad (Eds.) Teaching mathematics? Make it count. Proceedings of the Annual Conference of the Australian Council for Educational Research (pp. 47–52). Camberwell: ACER.

National Council of Teachers of Mathematics (2000). Executive summary. Retrieved February 2, 2015, from http://www.nctm.org/uploadedFiles/Math_ Standards/12752_exec_pssm.pdf

National Council of Teachers of Mathematics & National Association for the Education of Young Children (2010). Position paper on early childhood mathematics: Promoting good beginnings. Available online from http://www. naeyc.org/files/naeyc/file/positions/psmath.pdf

Perry, B. (2000). Early childhood numeracy. Australian Association of Mathematics Teachers. Retrieved February 2, 2015 from www.aamt.edu.au/content/ download/1252/25269/file/perry.pdf

Planty, M., Hussar, W., Snyder, T., Kena, G., Kewal Ramani, A., Kemp, J., Bianco, K., Dinkes, R. (2009). The Condition of Education 2009. Washingtonm, D.C.: National Center for Educational Statistics.

Poldrack, R. A., Clark, J., Pare-Blagoev, E.J., Shohamy, D., Creso Moyano, J., Myers, C. & Gluck, M.A. (2001). Interactive memory systems in the human brain. Nature, 414, 546–550.

Queensland Studies Authority (2006). Developing early mathematical understandings. Retrieved February 7, 2015, from www.qcaa.qld.edu.au/ downloads/p_10/ey_lt_maths_understandings.pdf

Reys, R. E., Lindquist, M., Lambdin, D. V. & Smith, N. L. (2012). Helping children learn mathematics (10th ed.). United States: John Wiley & Sons.

Renninger, K. A. (2000). Individual interest and its implications for understanding intrinsic motivation. In C. Sansone and J. M. Harackiewicz (Eds.) Intrinsic motivation: Controversies and new directions (pp. 373–404). San Diego, CA: Academic Press.

Rodionov, M. & Dedovets, Z. (2011). Increasing learner’s level of motivation in mathematics education through the use of uncomplicated situations. Literacy Information and Computer Education Journal, 2 (2), 366–371.

Roschelle, J. M., Pea, R. D., Hoadley, C. M., Gordin, D. N. & Means, B. M. (2000). Changing how and what children learn in school with computer-based technologies. The Future of Children: Children and Computer Technology, 10 (2), 76–101.

Runesson, U. (2005). Beyond discourse and interaction. Variation: A critical aspect for teaching and learning mathematics. Cambridge Journal of Education, 35 (1), 69–87.

Ryan, M. & Deci, E. L. (2000). Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemporary Educational Psychology, 25, 54–67.

Sullivan, P. (2011). Teaching mathematics using research-informed strategies. Camberwell, Vic: ACER Press.

Sullivan, P. & McDonough, A. (2007). Eliciting positive student motivation for learning mathematics. Mathematics: Essential Research, Essential Practice: 30th Annual Conference of the Mathematics Education Research Group of Australasia, 2, 698–707.

Taylor, L. & Adelman, H. (1999). Personalizing classroom instruction to account for motivational and developmental factors. Reading & Writing Quarterly, 15, 255–276.

Tiberius, R. & Tipping, J. (1990). Twelve principles of effective teaching and learning for which there is substantial empirical support. Toronto: University of Toronto.

Willis, J. (2014). Neuroscience reveals that boredom hurts: Students who seem to willfully defy admonishments to focus on their work may not be doing so intentionally but rather as a normal, age-appropriate brain reaction. Phi Delta Kappan. 95 (8), 28–32.

Click to download the Report as a PDF
View Mathseeds White Paper PDF